I. Vị trí tương đối của đường thẳng và mặt phẳng

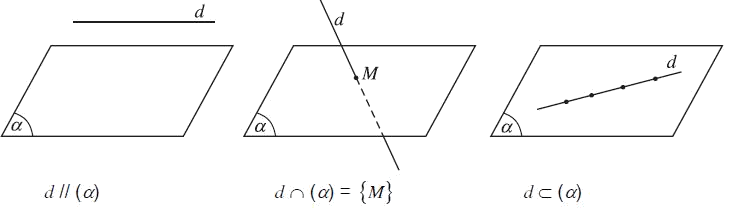
Giữa  đường thẳng d và mặt phẳng $\left( \alpha  \right)$ ta có ba vị trí tương đối như sau:

1. d và $\left( \alpha  \right)$ cắt nhau tại điểm M, ta kí hiệu $d \cap \left( \alpha  \right) = \left\{ M \right\}$;

2. d song song với $\left( \alpha  \right)$, ta kí hiệu $d//\left( \alpha  \right)$ hoặc $\left( \alpha  \right)//d$;

3. d nằm trong $\left( \alpha  \right)$, ta kí hiệu $d \subset \left( \alpha  \right)$.

II. Tính chất

* Định lí 1

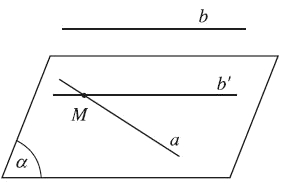
Nếu đường thẳng d không nằm trong mặt phẳng $\left( \alpha  \right)$ và d song song với đường thẳng d’ nằm trong $\left( \alpha  \right)$ thì d song song với $\left( \alpha  \right)$.  

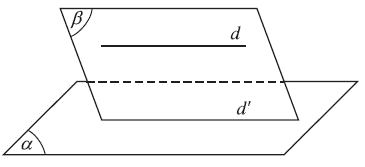
* Định lí 2

Cho đường thẳng a song song với mặt phẳng $\left( \alpha  \right)$. Nếu mặt phẳng $\left( \beta  \right)$ chứa a và cắt $\left( \alpha  \right)$ theo giao tuyến b thì b song song với a. 

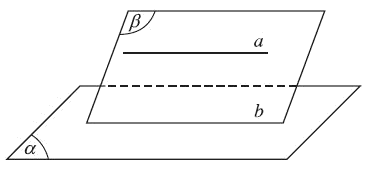
* Hệ quả

Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.

* Định lí 3

Cho hai đường thẳng chéo nhau. Có duy nhất mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.