GIẢI BÀI TẬP: Hình học
Cho tam giác OAB vuông cân tại O với OA = OB = 2a. Gọi (O) là đường tròn tâm O bán kính a.
Tìm điểm M thuộc (O) sao cho MA+2MB đạt giá trị nhỏ nhất.
Hướng dẫn giải
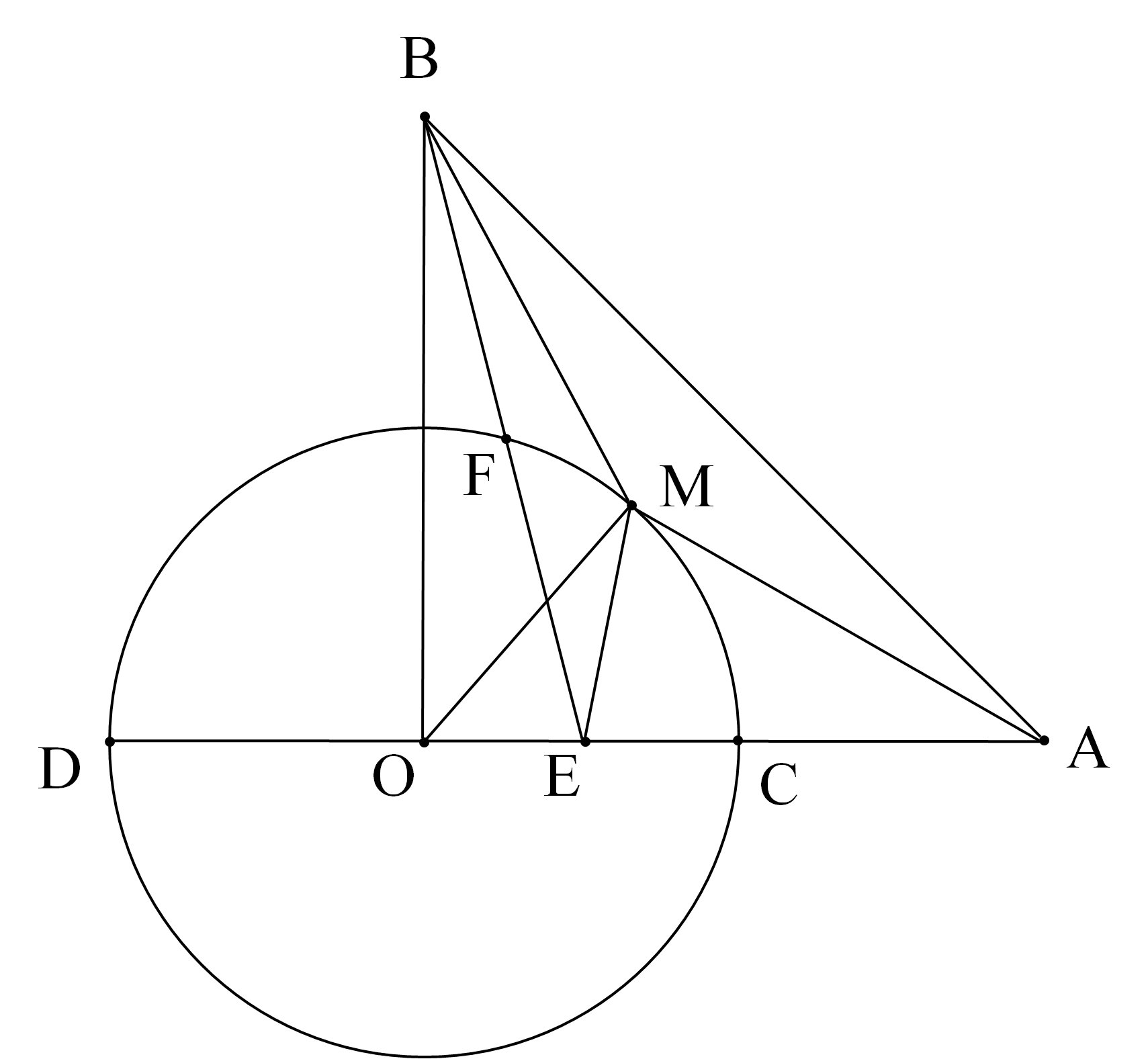
Đường thẳng OA cắt (O) tại C và D, với C là trung điểm của OA.
Gọi E là trung điểm của OC.
* Trường hợp M không trùng với C và D:
Hai tam giác OEM và OMA đồng dạng ( do $\widehat {MOE} = \widehat {AOM},\frac{{OM}}{{OA}} = \frac{1}{2} = \frac{{OE}}{{OM}}$)
$ \Rightarrow $ $\frac{{ME}}{{AM}} = \frac{{OM}}{{OA}} = \frac{1}{2} \Rightarrow MA = 2.EM$
* Trường hợp M trùng với C: MA=CA=2.EC=2.EM
* Trường hợp M trùng với D: MA=DA=2.ED=2.EM
Vậy
ta luôn có MA=2.EM
MA+2.MB = 2(EM+MB) $ \ge $ 2.EB = hằng số
Dấu
“=” xảy ra khi M là giao điểm của đoạn BE với đường tròn (O).
Vậy
MA+2.MB nhỏ nhất khi M là giao điểm của đoạn BE với đường tròn (O).



