I. ĐƯỜNG TIỆM CẬN NGANG

Cho hàm số $y = f\left( x \right)$ xác định trên một khoảng vô hạn (là khoảng dạng $\left( {a; + \infty } \right),\left( { - \infty ;b} \right);\left( { - \infty ; + \infty } \right)$. Đường thẳng $y = {y_o}$ là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số $y = f\left( x \right)$ nếu ít nhất một trong các điều kiện sau được thỏa mãn: 

$\mathop {\lim }\limits_{x \to  + \infty } f\left( x \right) = {y_o},\mathop {\lim }\limits_{x \to  - \infty } f\left( x \right) = {y_o}$

* Ví dụ: Quan sát đồ thị (C) của hàm số $y = \frac{1}{x} + 2$ 
              Nêu nhận xét khoảng cách từ điểm $M\left( {x;y} \right) \in \left( C \right)$ tới đường thẳng y = 2 khi $\left| x \right| \mapsto  + \infty $ và các giới hạn:

$\mathop {\lim }\limits_{x \to  + \infty } \left[ {f\left( x \right) - 2} \right],\mathop {\lim }\limits_{x \to  - \infty } \left[ {f\left( x \right) - 2} \right]$

Giải

Ta có M, M' lần lượt là các điểm thuộc (C) và đường thẳng y = 2 có cùng hoành độ x. Khi $\left| x \right|$ càng lớn thì các điểm M, M' trên đồ thị càng gần nhau.

$\begin{array}{l}
\mathop {\lim }\limits_{x \to  + \infty } \left[ {f\left( x \right) - 2} \right]\\
 = \mathop {\lim }\limits_{x \to  + \infty } \left[ {\left( {\frac{1}{x} + 2} \right) - 2} \right]\\
 = \mathop {\lim }\limits_{x \to  + \infty } \frac{1}{x} = 0
\end{array}$

Tương tự $\mathop {\lim }\limits_{x \to  - \infty } \left[ {f\left( x \right) - 2} \right] = 0$


 
II. ĐƯỜNG TIỆM CẬN ĐỨNG 

Đường thẳng $x = {x_o}$ được gọi là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số $y = f\left( x \right)$ nếu ít nhất một trong các điều kiện sau được thỏa mãn:

$\begin{array}{*{20}{l}} {\mathop {\lim }\limits_{x \to {x_o}^ + } f\left( x \right) =  + \infty ,\mathop {\lim }\limits_{x \to {x_o}^ - } f\left( x \right) =  - \infty }\\ {\mathop {\lim }\limits_{x \to {x_o}^ + } f\left( x \right) =  - \infty ,\mathop {\lim }\limits_{x \to {x_o}^ - } f\left( x \right) =  + \infty } \end{array}$

* Ví dụ: Tìm tiệm cận đứng của đồ thị hàm số $y = \frac{{x - 1}}{{x + 2}}$

Giải

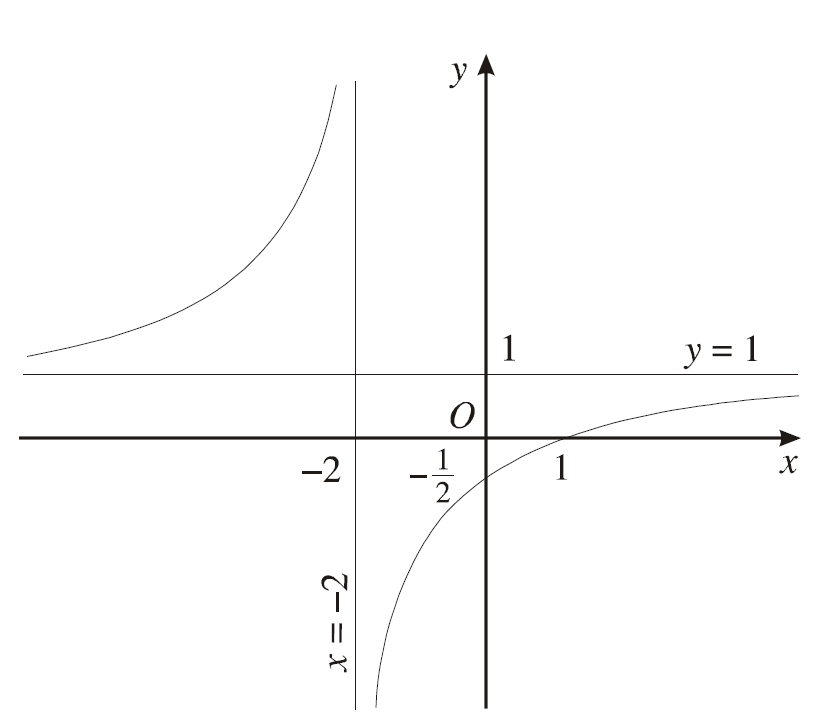
Vì $\mathop {\lim }\limits_{x \to  - {2^ + }} \frac{{x - 1}}{{x + 2}} =  - \infty $ nên đường thẳng x = -2 là tiệm cận đứng của (C).