I. ĐỊNH NGHĨA

Cho hàm số $y = f\left( x \right)$ xác định trên D.

a) Số M được gọi là giá trị lớn nhất của hàm số $y = f\left( x \right)$ trên tập D nếu $f\left( x \right) \le M$ với mọi x thuộc D và tồn tại ${x_0} \in D$ sao cho $f\left( {{x_0}} \right) = M$.

Kí hiệu $M = \mathop {\max }\limits_D f\left( x \right)$

b) Số m được gọi là giá trị lớn nhất của hàm số $y = f\left( x \right)$ trên tập D nếu $f\left( x \right) \ge m$ với mọi x thuộc D và tồn tại ${x_0} \in D$ sao cho $f\left( {{x_0}} \right) = m$.

Kí hiệu $M = \mathop {\min }\limits_D f\left( x \right)$.

II. CÁCH TÍNH GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ TRÊN MỘT ĐOẠN

* Định lí

Mọi hàm số liên tục trên một đoạn đều có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.

Cách tính giá trị lớn nhất và nhỏ nhất của hàm số, ta có 2 quy tắc sau:

1. Quy tắc 1 (sử dụng định nghĩa)

-  Giả sử f xác định trên $D \subset R$, ta có:

$\begin{array}{l}
M = \mathop {\max }\limits_{x \in D} f\left( x \right) \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{f\left( x \right) \le M,\forall x \in D}\\
{\exists {x_o} \in D:f\left( {{x_o}} \right) = M}
\end{array}} \right.\\
m = \mathop {\min }\limits_{x \in D} f\left( x \right) \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{f\left( x \right) \ge m,\forall x \in D}\\
{\exists {x_o} \in D:f\left( {{x_o}} \right) = m}
\end{array}} \right.
\end{array}$

2. Quy tắc 2 (Quy tắc tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn)

            Để tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f\left( x \right)$ xác định trên đoạn $\left[ {a;b} \right]$, ta làm như sau:

- Bước 1: Tìm các điểm ${x_1},{x_2},...,{x_n} \in \left( {a;b} \right)$ mà tại đó hàm số f có đạo hàm bằng 0 hoặc không có đạo hàm.

- Bước 2: Tính $f\left( {{x_1}} \right),f\left( {{x_2}} \right),...,f\left( {{x_n}} \right),f\left( a \right),f\left( b \right)$.

- Bước 3: so sánh các giá trị tìm được ở bước 2. Số lớn nhất trong các giá trị đó chính là giá trị lớn nhất của f trên đoạn $\left[ {a;b} \right]$; số nhỏ nhất trong các giá trị đó chính là giá trị nhỏ nhất của f trên đoạn $\left[ {a;b} \right]$.

Ví dụ: Tính giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y = \sin x$ trên đoạn $\left[ {\frac{\pi }{6};\frac{{7\pi }}{6}} \right]$.

Giải

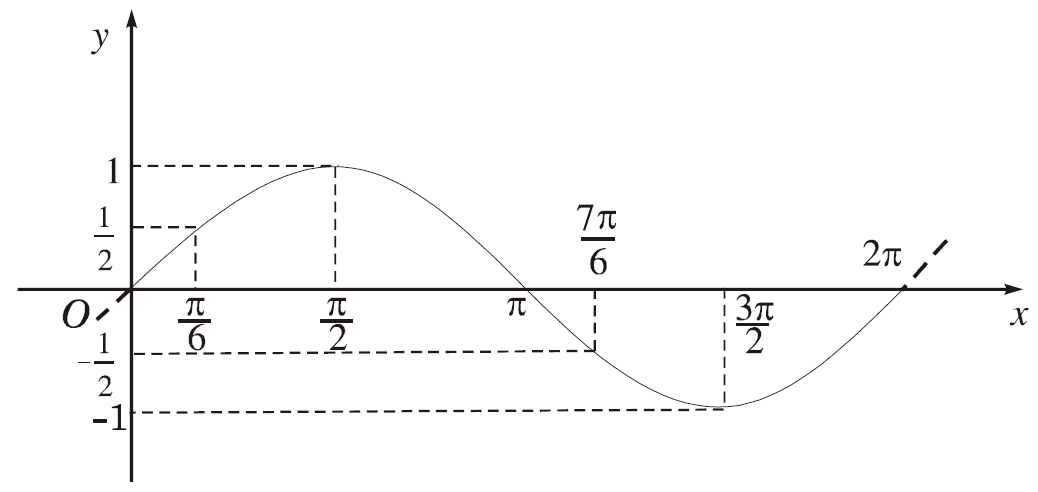
Từ đồ thị của hàm số số $y = \sin x$, ta thấy ngay:

Trên đoạn $\left[ {\frac{\pi }{6};\frac{{7\pi }}{6}} \right]$, ta có:

$y\left( {\frac{\pi }{6}} \right) = \frac{1}{2};y\left( {\frac{\pi }{2}} \right) = 1$

Và $y\left( {\frac{{7\pi }}{6}} \right) =  - \frac{1}{2}$