GIẢI BÀI TẬP: Đại số
Cho parabol $\left( P \right):y = {x^2}$ và đường thẳng $\left( d \right):y = 3x - 2.$
a) Vẽ $(P)$ và $(d)$ trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của $(P)$ và $(d)$ bằng phép tính.
a) Vẽ $(P)$ và $(d)$ trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của $(P)$ và $(d)$ bằng phép tính.
Hướng dẫn giải
a) Parabol $(P)$ có bảng giá trị:
Đường thẳng $(d)$ đi qua các điểm $(0;-2)$ và $\left( {\frac{2}{3};0} \right).$
Vẽ $(P)$ và $(d)$ trên cùng hệ trục tọa độ.
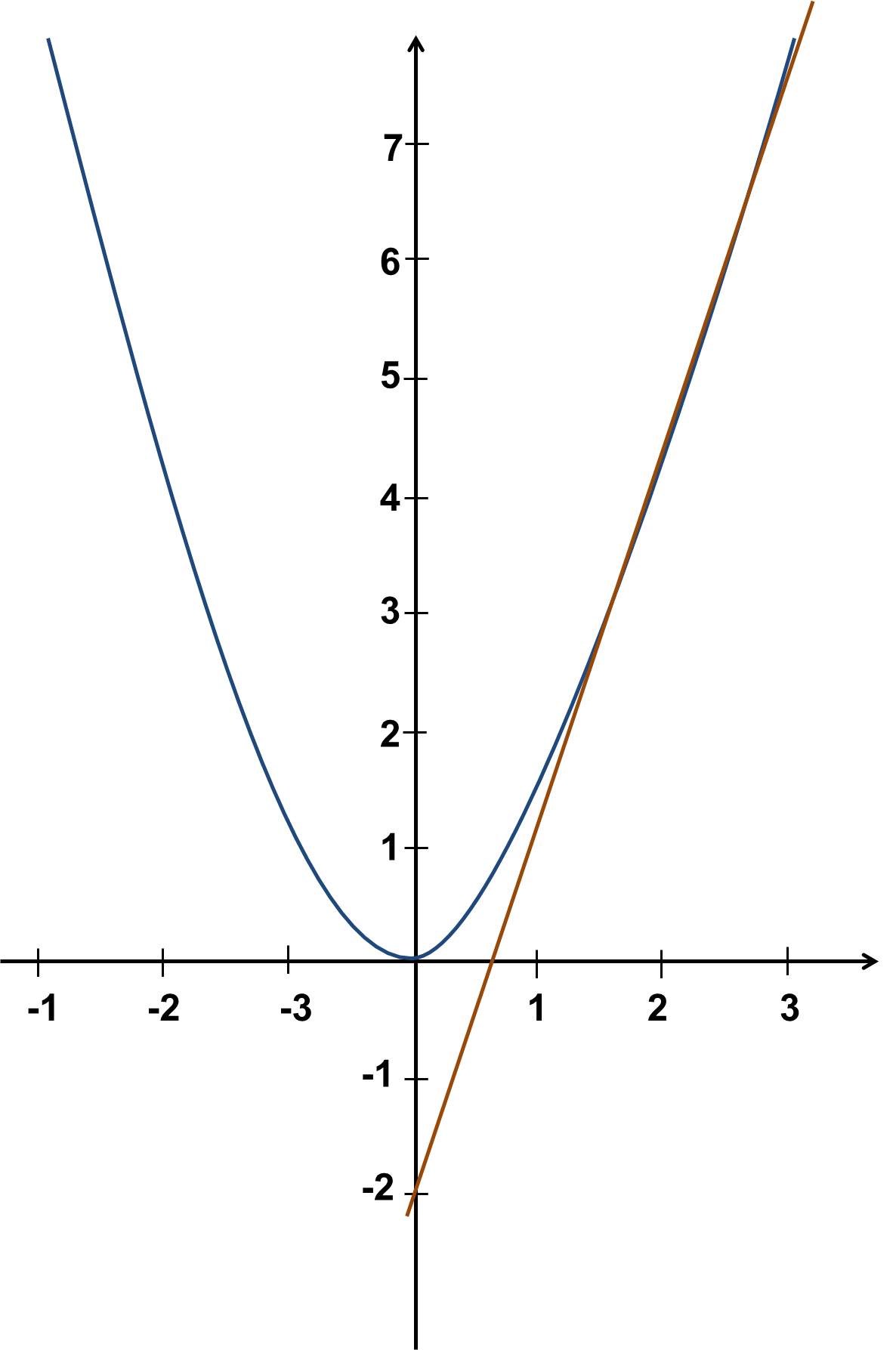
b) Phương trình hoành độ giao điểm của $(P)$ và $(d)$:
${x^2} = 3x - 2 \Leftrightarrow {x^2} - 3x + 2 = 0.$
Vì $a+b+c=1+(-3)+2=0$ nên phương trình có 2 nghiệm phân biệt là:
$\left\{ \begin{array}{l}
{x_1} = 1 \Rightarrow {y_1} = 1\\
{x_2} = 2 \Rightarrow {y_2} = 4
\end{array} \right.$
Vậy $(P)$ cắt $(d)$ tại 2 điểm có tọa độ $(1;1)$ và (2;4).$
| x | -2 | -1 | 0 | 1 | 2 |
| y | 4 | 1 | 0 | 1 | 3 |
Vẽ $(P)$ và $(d)$ trên cùng hệ trục tọa độ.

b) Phương trình hoành độ giao điểm của $(P)$ và $(d)$:
${x^2} = 3x - 2 \Leftrightarrow {x^2} - 3x + 2 = 0.$
Vì $a+b+c=1+(-3)+2=0$ nên phương trình có 2 nghiệm phân biệt là:
$\left\{ \begin{array}{l}
{x_1} = 1 \Rightarrow {y_1} = 1\\
{x_2} = 2 \Rightarrow {y_2} = 4
\end{array} \right.$
Vậy $(P)$ cắt $(d)$ tại 2 điểm có tọa độ $(1;1)$ và (2;4).$



