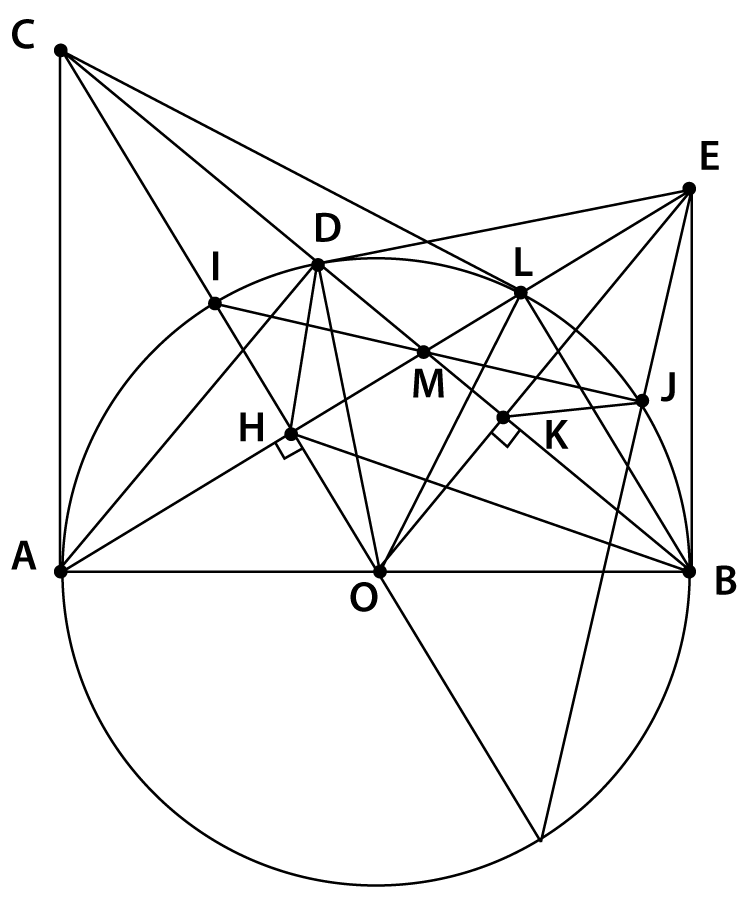
a) Chứng minh: Tứ giác ACDH nội tiếp và $\widehat {CHD} = \widehat {ACB}$.

$\widehat {ADB} = {90^0}$ (góc nội tiếp chắn nửa đường tròn)

$ \Rightarrow \widehat {ADC} = {90^0}$

$ \Rightarrow \widehat {ADC} = \widehat {AHC}$

$ \Rightarrow $ Tứ giác ACDH nội tiếp.

$ \Rightarrow \widehat {CHD} = \widehat {CAD}$

mà $\widehat {CAD} = \widehat {ABC}$.

nên $\widehat {CHD} = \widehat {ABC}$.


b) Chứng minh: Hai tam giác OBH và OBC đồng dạng với nhau và HM là tia phân giác của góc BHD.
Ta có:
$OH.OC = O{A^2} = O{B^2}$

$ \Rightarrow \frac{{OH}}{{OB}} = \frac{{OB}}{{OC}}$

$ \Rightarrow \Delta OHB$ đồng dạng $\Delta OBC$ (cạnh góc cạnh).

$ \Rightarrow \widehat {OHB} = \widehat {OBC}$

$ \Rightarrow \widehat {OHB} = \widehat {CHD}$

$ \Rightarrow \widehat {BHM} = \widehat {DHM}$

hay HM là đường phân giác của góc BHD.

c) Chứng minh
MD.BC=MB.CD và MB.MD=MK.MC

Tam giác DHB có HM là phân giác trong
$ \Rightarrow \frac{{MD}}{{MB}} = \frac{{HD}}{{HB}}$

Tam giác DHB có HC là phân giác ngoài
$\Rightarrow \frac{{CD}}{{CB}} = \frac{{HD}}{{HB}}$

Vậy $\frac{{MD}}{{MB}} = \frac{{CD}}{{CB}} \Rightarrow $ MD.BC=MB.CD

Cách 1:
Từ trên $MD.(MB+MC)=MB.(MC-MD)$

$ \Rightarrow  2MB.MD=MC(MB-MD)$

$ \Rightarrow  2MB.MD=2MK.MC$  

$ \Rightarrow  MB.MD=MK.MC$

Cách 2:
Gọi L là giao điểm của AE với đường tròn (O).

5 điểm A, O, K, L, C cùng thuộc đường tròn.

$ \Rightarrow  MK.MC=MA.ML$

Mà $MA.ML=MB.MD$

$ \Rightarrow  MB.MD = MK.MC$ 


d) Chứng minh: Hai đường thẳng OC và EJ cắt nhau tại một điểm nằm trên (O).
Gọi N là giao điểm của CO với đường tròn(O).

$ \Rightarrow \widehat {IJN} = {90^0}$  (1)

Mặt khác: $MI.MJ=MD.MB=MK.MC$

$ \Rightarrow \Delta MIC $ đồng dạng $\Delta MKJ$

$\Rightarrow \widehat {MCI} = \widehat {MJK} = \widehat {MEO}$

$ \Rightarrow $ MEJK nội tiếp.

$\Rightarrow \widehat {EJM} = {90^0}$   (2)

Từ (1) và (2) suy ra E, J, N thẳng hàng.

$ \Rightarrow $ Hai đường thẳng OC và EJ cắt nhau tại một điểm nằm trên (O).